Concentric Circles on a Map, version 3
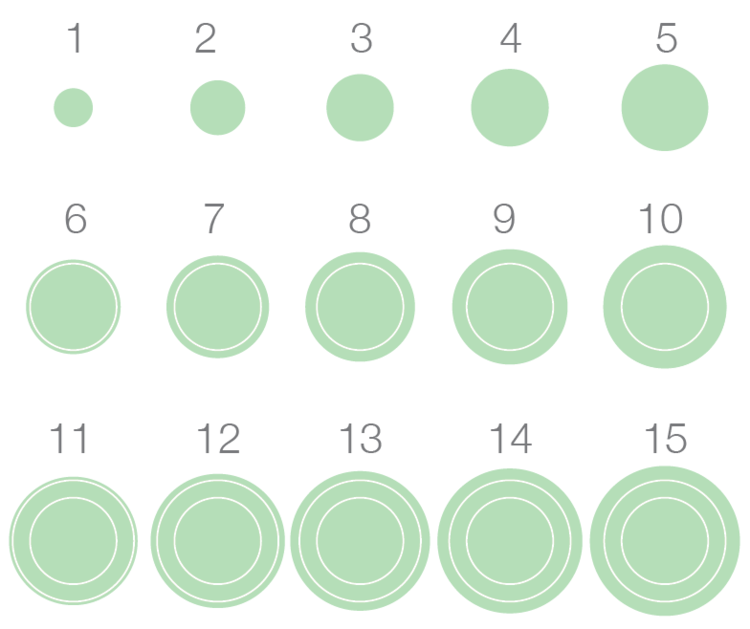
After my attempt at improving the concentric circles, Stephen Few was kind enough to provide more feedback: he still doesn’t like them. Your experiments with concentric circles are interesting and it’s clear that you’re having fun exploring this, but the new version doesn’t seem to work any better than the first, even though you’ve eliminated […]
Concentric Circles on a Map, version 2.0
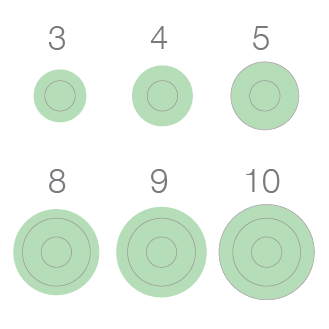
In response to Stephen Few’s challenge to do better than his bricks to display quantities on a map, I proposed the concentric circles. He shot down version 1.0: Thanks for exploring the possibilities of concentric circles. Unfortunately, as you’ve seen, when there are more than three or four concentric circles, we cannot perceive the quantities […]
Concentric Circles on a Map
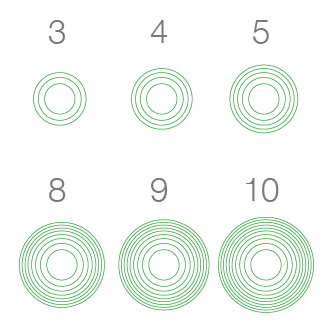
Stephen Few introduced “bricks” a few days ago as a new way to display quantities on a map. Using circles is tricky because humans are not skilled at distinguishing areas. Few suggests that we can distinguish the shape of the bricks arrangement and hence count them more easily (“preattentively”). The problem arises when bricks overlap, […]